Lösung der Aufgabe B 2.1
Aufgabe B 2.1
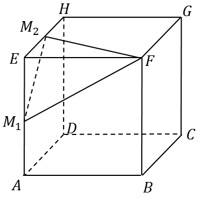
In einem würfelförmigen Ausstellungsraum mit der
Kantenlänge 8 Meter ist ein dreieckiges Segeltuch
aufgespannt.
Es ist im Punkt F sowie in den Kantenmitten M1
und M2 befestigt (siehe Abbildung).
Es wird angenommen, dass das Segeltuch nicht
durchhängt.
In einem Koordinatensystem stellen die Punkte A(8|0|0), C(0|8|0) und H(0|0|8)
die entsprechenden Ecken des Raumes dar.
a) Bestimmen Sie eine Koordinatengleichung der Ebene S, in der das Segeltuch liegt.
Zeigen Sie, dass das Segeltuch die Form eines gleichschenkligen Dreiecks hat.
Berechnen Sie den Flächeninhalt des Segeltuchs.
Welchen Abstand hat das Segeltuch von der Ecke E?
(Teilergebnis: S: 2x1-x2+2x3=24)
(6 VP)
b) Auf der Diagonalen AC steht eine 6 Meter hohe Stange senkrecht auf dem Boden.Das obere Ende der Stange berührt das Segeltuch.
In welchem Punkt befindet sich das untere Ende der Stange?
(3 VP)
Aufgabe B 2.2
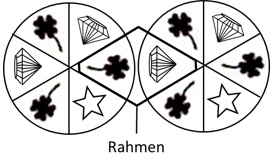
Auf zwei Glücksrädern befinden sich jeweils sechs gleich große Felder. Bei jedem Spiel werden die Räder einmal in Drehung versetzt. Sie laufen dann unabhängig voneinander aus und bleiben so stehen, dass von jedem Rad genau ein Feld im Rahmen sichtbar ist.
a) Zunächst werden die Räder als ideal angenommen.
Bei einem Einsatz von 0,20 € sind folgende Auszahlungen vorgesehen:
Stern - Stern 2,00 €
Diamant - Diamant 0,85 €
Kleeblatt - Kleeblatt 0,20 €
In allen anderen Fällen wird nichts ausbezahlt.
Weisen Sie nach, dass das Spiel fair ist.
Nun möchte der Veranstalter auf lange Sicht pro Spiel 5 Cent Gewinn erzielen. Dazu soll nur der Auszahlungsbetrag für "Diamant - Diamant" geändert werden. Berechnen Sie diesen neuen Auszahlungsbetrag.
(3 VP)
b) Es besteht der Verdacht, dass die Wahrscheinlichkeit p für "Stern - Stern" geringer als 1/36 ist. Daher soll ein Test mit 500 Spielen durchgeführt werden.Formulieren Sie die Entscheidungsregel für die Nullhypothese H0: p≥1/36, wenn die Irrtumswahrscheinlichkeit höchstens 5% betragen soll.
(3 VP)
Lösung der Aufgabe B 2.2